특이값 분해(Singular Value Decomposition, SVD)

Notice

Recent Posts

Recent Comments

Link

« 2024/12 »
일	월	화	수	목	금	토
1	2	3	4	5	6	7
8	9	10	11	12	13	14
15	16	17	18	19	20	21
22	23	24	25	26	27	28
29	30	31

Tags more

Archives

Today

Total

관리 메뉴

Studying data

특이값 분해(Singular Value Decomposition, SVD) 본문

선형대수

특이값 분해(Singular Value Decomposition, SVD)

halloweenie 2022. 12. 1. 12:33

1. 특이값 분해 (Singular Value Decomposition, SVD)

선형대수에서 특이값 분해(Singular Value Decomposition, SVD)란 행렬 분해(Matrix Factorization), 행렬을 대각화하는 방법 중 하나로, 행렬을 직교행렬(orthogonal matrix)과 대각행렬(diagonal matrix)로 분해하는 방법이다. 즉 행렬을 차원축소하는 도구인데 실제로 주성분 분석(PCA)과 같은 분야에서 흔하게 쓰인다. 이 방법은 고유값 분해(eigen decomposition)의 일반화 된 방식이라고 볼 수 있다. 고유값 분해가 \(m \times m\)의 정방행렬 중에서도 m개의 고유벡터들이 선형독립인 경우에만 가능한 방법이었다면, 특이값 분해는 정방행렬 여부에 관계없이 모든 \(m \times n\)직사각형 행렬에 대해 적용 가능한 방법이다. 즉, 특이값 분해를 이용하면 어떤 종류의 행렬이라도 분해가 가능하다.

2. 특이값 분해의 기준행렬

행렬 A의 크기가 \(n \times d\)라는 말은 \(d\)차원에서 \(n\)개의 점이 있다고 생각할 수 있다. 따라서 \(n \times p\)행렬 A에 대한 차원축소란 \(n\)개의 점을 표현할 수 있는 \(p\)보다 작은 차원인 \(d\)차원-부분공간을 찾는 문제라고 볼 수 있다. 해당 부분공간은 데이터와 부분 공간으로부터의 수직거리를 최소화 시켜서 구할 수 있다. 이때 직선거리의 최소화는 회귀분석에 나오는 제곱합(sum of squres)을 최소화 시키는 것인데 제곱합이라고 했으니 \(A^{T}A\), \(AA^{T}\) 를 사용하는 것이고, 따라서 특이값 분해에서는 원본행렬 A 자체를 다루기보다는 \(A^{T}A\), \(AA^{T}\) 를 다루는 것이다.

또한 \(AA^{T}\)는 A의 행의 내적이라고 볼 수 있기 때문에 이는 A의 행과 원점과의 거리를 나타내는 것이고, \(A^{T}A\)는 A의 열의 내적이라고 볼 수 있기 때문에 이는 A의 열과 원점과의 거리라고 볼 수 있다. 참고로 어떤 행렬과 그 행렬의 전치행렬의 곱은 항상 대칭행렬이므로 \(A^{T}A\), \(AA^{T}\) 는 모두 대칭행렬이고 대칭행렬은 항상 고유값 분해가 가능하다.

3. 특이값(singular value)

행렬의 고유값에 루트를 씌운 것 \(\sqrt{\lambda}\)이 특이값(singular value)이다. 예를 들어 \(n \times p\) 행렬 A에 대해 \(A^{T}A\)의 고유값을 \(\lambda_1, \lambda_2, ..., \lambda_p\) 라고 하면 \(\sigma_1 = \sqrt{\lambda_1}, \sigma_2 = \sqrt{\lambda_2}, ..., \sigma_p = \sqrt{\lambda_p}\)를 A의 특이값이라고 한다. \(m \times n\) 행렬 A의 특이값 개수는 min(m, n)개이다.

4. 특이값 분해 과정

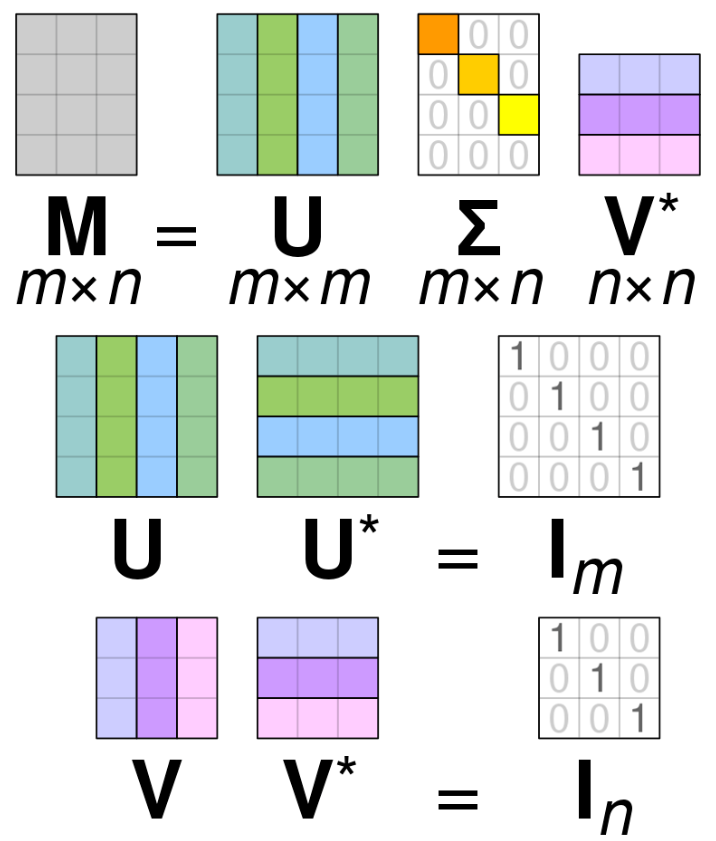
그럼 이제 실제로 \(n \times p\) 행렬 A의 특이값 분해가 어떻게 이루어지는지 살펴보자. 특이값 분해는 다음과 같이 표현한다.

• \(U\) : \(n \times n\) 크기의 *직교행렬(orthogonal matrix)로 \(AA^{T}\)의 고유벡터를 단위벡터로 만든 것(*벡터의 정규화)을 열벡터로 구성하며 left singular vector라 부른다. 큰 고유값에 대응되는 고유벡터가 항상 왼쪽에 위치한다.

• \(V^T\) : \(p \times p\) 크기의 직교행렬로 \(A^{T}A\)의 고유벡터를 단위벡터로 만든 것(벡터의 정규화)을 열벡터로 구성한 행렬을 전치한 것이며 right singular vector라 부른다. 큰 고유값에 대응되는 고유벡터가 항상 왼쪽에 위치한 상태에서 전치시킨다.

• \(\Sigma\) : \(AA^{T}\) 또는 \(A^{T}A\)의 특이값들(=각 고유값들의 제곱근)을 각 대각원소로 두고, 나머지를 0으로 채운 \(n \times p\) 크기의 직사각 대각행렬(diagonal matrix)이다. (💡\(AA^{T}\)와 \(A^{T}A\)의 0을 제외한 고유값들은 서로 같으며 항상 모두 0 이상이므로 루트를 씌울 수 있다. 또, 고유값이 같으므로 특이값도 같다.) \(\Sigma\)의 대각원소들을 A의 특이값이라 부른다. 큰 특이값이 항상 왼쪽부터 위치한다.

💡 \(AA^{T}\)와 \(A^{T}A\)의 ii)0을 제외한 고유값들은 서로 같으며 i)항상 모두 0 이상인 것의 증명 (더보기 클릭)

i) \(A^TA\)의 고유값을 \(λ\), 고유벡터를 v (v≠0)라 했을 때, \(A^TAv = λv\) 이다. 양변에 \(v^T\)를 곱해보면 \(v^TA^TAv = λv^Tv\)에서 \((Av)^TAv = λv^Tv\) 즉, \(∥Av∥^2 = λ∥v∥^2\) 이므로 λ≥0 이다.

ii) \(A^TA\)의 0이 아닌 고유값을 λ, 고유벡터를 v (v≠0)라 했을 때, 정의에 의해 \((A^TA)v=λv\)이다. 양변에 A를 곱해보면 \(A(A^TA)v = λAv\) 즉, \(AA^T(Av) = λ(Av)\)이므로 Av≠0라면 λ는 또한 \(AA^T\)의 고유값임을 알 수 있다. 그런데, 만일 Av=0라 하면 \((A^TA)v=λv\)에서 λ=0이어야 하므로 Av≠0이다. 동일한 방식으로 \(AA^T\)의 0이 아닌 모든 고유값도 또한 \(A^TA\)의 고유값이 됨을 쉽게 보일 수 있다.

참고: https://darkpgmr.tistory.com/106

\(m \times n\)행렬에서

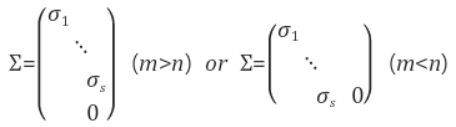
*벡터의 정규화: 벡터를 단위벡터로 만드는 것 (더보기 클릭)

*직교 행렬(orthogonal matrix)은 행벡터와 열벡터가 유클리드 공간의 "정규 직교 기저"를 이루는 실수 행렬이다. 즉, 행렬의 행과 열벡터들이 자기 자신을 제외한 나머지 모든 행, 열벡터들과 직교(perpendicular)이면서 동시에 단위 벡터(unit vector)인 행렬을 의미한다. ('정규'는 단위벡터임을 의미)

*\(AA^{T}\), \(A^{T}A\)는 각각 대칭행렬이고, 대칭행렬의 고유벡터들은 서로 직교(orthogonal)한다. 이 직교하는 고유벡터들을 단위벡터로 만들어(정규화) 열벡터로 구성한 것이 \(U\), \(V^T\) 이고 \(U\), \(V^T\) 는 모두 직교행렬이다. (직교행렬의 전치행렬은 직교행렬)

만약 특정 행렬이 양의 값을 가지고 정방행렬일 경우, 고유값 분해와 특이값 분해는 같아진다.

직교행렬의 성질

\(n \times n\)의 정방행렬 \(Q\)가 직교행렬이면 \(QQ^T = Q^TQ = 1_{n \times n}\)이고 \(Q\)의 전치행렬과 역행렬은 같다( \(Q^T = Q^{-1}\)). 즉, 직교행렬의 전치행렬과 역행렬은 같다.

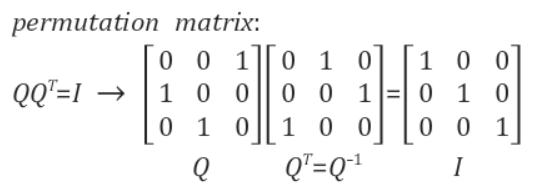
\(m \times n\) 행렬의 특이값 분해에서 \(U\)와 \(V^T\)는 모두 직교행렬이므로 아래가 성립한다.

\(UU^T = I_m\)

\(VV^T = I_n\)

\(U^T = U^{-1}\)

\(V^T = V^{-1}\)

5. 특이값 분해의 기하학적 의미

https://darkpgmr.tistory.com/106 에서 가져온 내용

행렬을 x' = Ax와 같이 좌표공간에서의 선형변환으로 봤을 때 직교행렬(orthogonal matrix)의 기하학적 의미는 회전변환(rotation transformation) 또는 반전된(reflected) 회전변환, 대각행렬(diagonal maxtrix)의 기하학적 의미는 각 좌표성분으로의 스케일변환(scale transformation)이다.

행렬 R이 직교행렬(orthogonal matrix)이라면 \(RR^T = E\)이다. 따라서 \(det(RR^T) = det(R)det(R^T) = det(R)^2 = 1\)이므로 det(R)는 항상 +1, 또는 -1이다. 즉, 직교행렬의 행렬식은 +1 또는 -1이다. 만일 det(R)=1이면 이 직교행렬은 회전변환을 나타내고 det(R)=-1이라면 뒤집혀진(reflected) 회전변환을 나타낸다.

따라서 \(A = UΣV^T\)에서 U, V는 직교행렬, Σ는 대각행렬이므로 Ax는 x를 먼저 \(V^T\)에 의해 회전시킨 후 Σ로 스케일을 변화시키고, 다시 U로 회전시키는 것임을 알 수 있다. 즉, 행렬의 특이값(singular value)이란 이 행렬로 표현되는 선형변환의 스케일 변환을 나타내는 값으로 해석할 수 있다.

6. Reduced SVD와 행렬근사, 데이터 압축

https://darkpgmr.tistory.com/106 에서 가져온 내용

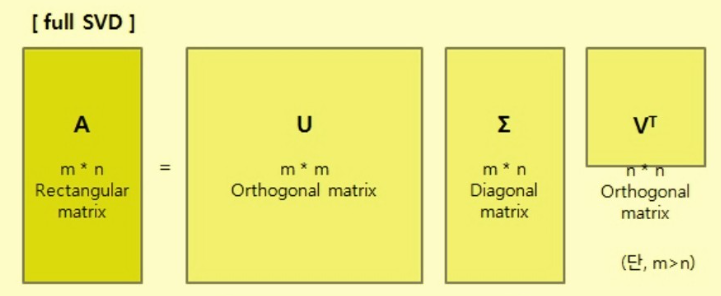
full SVD

아래와 같이 m×n 행렬 A를 SVD로 분해하는 것을 full SVD라 부른다 (단, m>n)

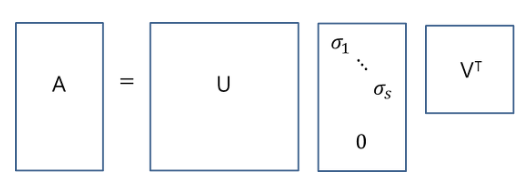
reduced SVD

그런데 실제로 이와같이 full SVD를 하는 경우는 드물며, 아래 그림들과 같이 reduced SVD를 하는게 일반적이다 (s=n개의 singular value들 중 0이 아닌 것들의 개수가 r개, t<r라고 가정).

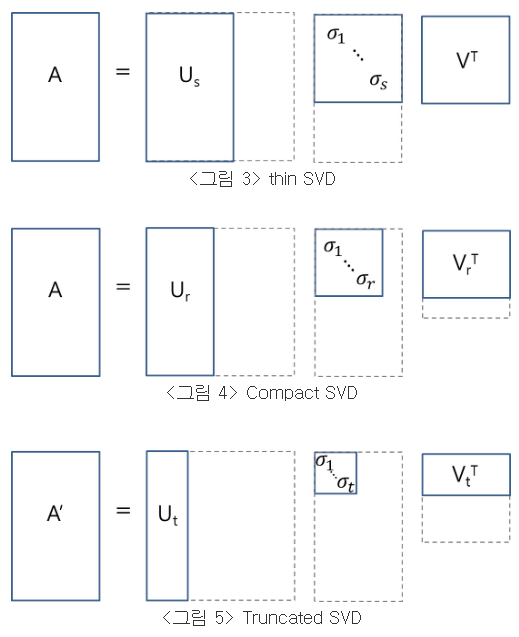
<그림 3>의 thin SVD는 Σ에서 대각파트가 아닌 0으로 구성된 부분을 없애고 U에서는 이에 대응되는 열벡터들를 제거한 형태이고, <그림 4>의 compact SVD는 비대각 원소들뿐만 아니라 0인 특이값(\(\sigma\))들과 그에 대응되는 열벡터들까지 모두 제거한 형태이다. 이때, 이렇게 계산된 A가 원래의 A와 동일한 행렬이 나옴은 쉽게 확인할 수 있다. 그러나 <그림 5>의 truncated SVD는 0이 아닌 특이값까지 제거한 형태로, 이 경우에는 원래의 A가 보존되지 않고 A에 대한 근사행렬 A'가 나온다.

truncated SVD로 근사한 행렬 A'는 matrix norm ∥A-A'∥을 최소화시키는 rank t 행렬로서 데이터 압축, 노이즈제거 등에 활용될 수 있다.

데이터 압축의 한 예로 아래와 같은 600 × 367 이미지를 SVD로 압축해 보자.

이 이미지의 픽셀값을 원소값으로 하는 600 × 367 행렬 A를 잡고 SVD를 한 후, truncated SVD를 이용하여 근사행렬 A'을 구한 후 이를 다시 이미지로 표시해 보면 다음과 같다 (통상적인 m>n 형태로 만들기 위해 원래 이미지를 90도 회전시킨 후 SVD를 적용. 367 × 600 → 600 × 367).

t = 20인 <그림 9>의 경우, 데이터 압축율은 8.8%이다. 원래 이미지를 표현하기 위해서는 367*600 = 220,200의 메모리가 필요하다. 그런데 <그림 9> t = 20인 경우에는 600*367(원본 90도 회전)(A') = 600*20(U) + 20(Σ) + 20*367(\(V^T\)) = 19,360이므로 압축률은 19,360/220,200*100 = 8.8% 이다. 화질을 보면 좋은 압축 방법은 아님을 알 수 있지만 truncated SVD를 통한 데이터 근사가 원래의 데이터 핵심을 잘 잡아내고 있음을 알 수 있다.