카이제곱 독립성 검정(Chi-Square Test for Independence), Scipy.stats의 chi2_contingency()

카이제곱 독립성 검정(Chi-Square Test for Independence, Two-Sample)

카이제곱 독립성 검정은 두 가지 범주형 또는 명목형 변수가 관련될 가능성 여부를 확인하는 데 사용하는 통계적 가설 검정 방법이다. 즉, 두 변수가 연관이 있는지, 무관한지를 검증하는 방법이다. (질적 변수 = 범주형 변수   ⊃   명목형 변수)

 

먼저 두 변수가 서로 독립적이라(무관하다) 가정하고 검정을 통해 이 가정이 타당한지의 여부를 밝힌다.

 

H₀: 두 변수는 서로 무관하다.

H_a: 두 변수는 서로 연관이 있다.

 

카이제곱 독립성 검정의 예

• 성별(남, 여)과 정당 선호도(공화당, 민주당, 무소속) 간에 통계적으로 연관이 있는지 무작위로 100명의 사람들 조사
• 학년(1학년, 2학년, 3학년)과 선호하는 영화 장르(액션, 판타지, 로맨스, 호러) 간에 연관이 있는지 한 학교의 각 학년에서 100명씩 무작위로 조사
• 선호하는 스포츠(농구, 야구, 축구, 수영)와 유년기를 보낸 곳(도시, 시골) 간에 통계적으로 연관이 있는지 무작위로 100명의 사람들 조사

 

카이제곱 독립성 검정 예제

가설과 α값 설정 

 

뱃속에 있는 아기의 성별이 아기의 심장박동수와 연관이 있으며, 여자 아이일수록 높은 심장박동수를 갖는다는 이론이 있다. 이 이론을 검증하고자 하여 40명의 산모의 출산 전 마지막 검사에서 각 아기들의 심장박동수를 측정한다. 그리고 이 랜덤하게 선정된 40개의 측정치에서 우리는 1)성별과 2)심장박동수라는 두 변수값을 얻는다. 성별은 여자, 남자라는 두 개의 범주를 갖는다. 심장박동수는 continuous한 값이므로 이를 145라는 기준 심박수를 정해, 그것을 기준으로 low와 high, 두 가지로 범주화한다. 

여기서 검증하고자 하는 것은 "성별과 심장박동수가 연관이 있다"라는 것이므로 다음과 같이 가설을 설정한다. 유의수준 α는 0.1로 설정한다.

 

H₀: 아기의 성별과 심장박동수는 연관이 없다.

H_a: 아기의 성별과 심장박동수는 연관이 있다.

 

 

기대 빈도 계산

 

40개의 측정값으로 contingency table을 만든다. 

 

관측값 contingency table

위와 같은 과정으로 각 셀의 기대 빈도(E)를 계산한다.

관측값과 기대빈도

 

 

카이제곱값 계산

 

카이제곱값을 계산하면 다음과 같다.

 

 

만약 계산한 카이제곱값이 임계값보다 크다면 귀무가설을 기각하게 되고, 아기의 성별과 심박수는 연관이 있다는 결론에 이르게 된다.

 

df = (Heart Rate 범주의 수 - 1) X (Gender 범주의 수 - 1) = 1 X 1 = 1이고,

α = 0.1로 설정했기 때문에 다음 표에 의해 임계값은 X²_α = X²_0.10 =  2.706이 된다.

카이제곱 분포의 임계값

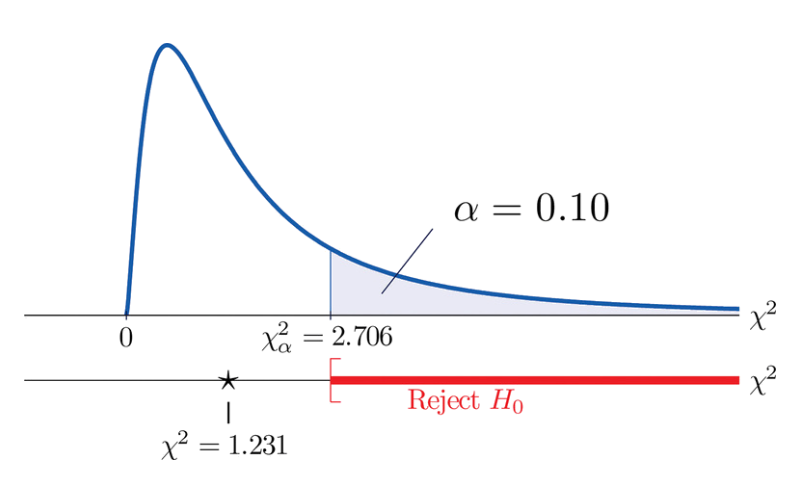
귀무가설의 기각역은 [2.706, ∞) 가 된다.

결국, 카이제곱값(χ²)은 임계값(X²_0.10)보다 작으므로 귀무가설을 기각하지 않고 (p-value > 0.10)

아기의 성별과 심박수는 연관이 없다 는 결론에 이르게 된다.

 

Scipy를 이용한 카이제곱 독립성 검정

실제로 scipy.stats의 chi2_contingency()를 이용해 독립성 검정을 해보면 다음과 같은 결과가 나온다.

import numpy as np
from scipy.stats import chi2_contingency

# contingency table
baby = np.array([11, 7, 17, 5]).reshape(2,2)

# chi-square test of independence
chi2_contingency(baby, correction=False)

# result
(1.2313612313612308, 0.2671424742403274, 1, array([[12.6,  5.4], [15.4,  6.6]]))

X² : 1.2313612313612308

p-value : 0.2671424742403274

degree of freedom : 1

E(기대빈도) : array([[12.6, 5.4], [15.4, 6.6]])

 

p-value > 0.10 이므로 귀무가설을 기각하지 않는다.

 

 

 

 

 

 

Reference

https://stats.libretexts.org/Bookshelves/Introductory_Statistics/Book%3A_Introductory_Statistics_(Shafer_and_Zhang)/11%3A_Chi-Square_Tests_and_F-Tests/11.01%3A_Chi-Square_Tests_for_Independence