Studying data
[이상치 탐색] 2. ML을 통한 Outlier Detection - (1) DBSCAN (with scikit-learn) 본문
[이상치 탐색] 2. ML을 통한 Outlier Detection - (1) DBSCAN (with scikit-learn)
halloweenie 2023. 4. 29. 20:14앞선 "1. 통계값을 이용한 Outlier Detection"에 이어 머신러닝 알고리즘을 통한 이상치 탐색 방법을 소개하는 포스팅의 시작이다. 대부분의 머신러닝 데이터셋은 크기가 크며, 특성의 수가 많고(고차원) 또 특성 간에 어떤 복잡한 관계가 있는지 아직 알 수 없기 때문에 표준편차나 사분위수 같은 간단한 통계값을 사용해 이상치를 탐색하는 것은 한계가 있다고 한다. 따라서 자동적으로 이상치를 탐색해주는 methods, 알고리즘을 사용한다.
DBSCAN (Density-Based Spatial Clustering of Applications with Noise)
IQR, Z-score는 모두 일변량(Univariate) 이상치 감지를 위한 방법들인 반면, DBSCAN은 다변량(Multivariate) 분석에서의 이상치 감지에 쓰인다. (종속변수의 수에 따라 일변량, 이변량, 다변량 데이터로 구분됨) 클러스터 수를 미리 지정할 필요가 없다는 점을 제외하면 k-means와 같다.
Clustering with DBSCAN
클러스터링 작업을 수행하는 접근 방식과 알고리즘은 크게 3가지로 분류된다.
- 파티션 기반 (Partition-based) 클러스터링: k-means, k-median
- 계층적 (Hierarchical) 클러스터링: Agglomerative, Divisive
- 밀도 기반 (Density-based) 클러스터링: DBSCAN
파티션 기반과 계층적 클러스터링은 원형이나 convex 형태의 일반적인 모양으로 된 클러스터에서 효율적이다. 즉, compact하고 잘 분리되어 있는 클러스터에서 잘 작동하는 것인데, 노이즈와 이상치에 영향을 많이 받는다는 단점이 있다. 아래 그림의 데이터셋은 k-means 알고리즘을 사용해 쉽게 3개의 클러스터로 나뉘어졌다.

하지만 실세계의 데이터는 원형(convex)으로만 잘 분리되지는 않으며 이상치를 포함하고 있다. 아래 그림들처럼 형태가 일반적이지 않고 임의의 모양(ex. 겹으로 된 oval, linear, "S" shaped)으로 된 클러스터의 경우 밀도 기반 클러스터링이 더 효율적이다.



아래 그림에서 k-means와 DBSCAN의 클러스터링 결과 차이를 보면 irregular한 임의의 형태로 된 데이터셋에서 k-means의 클러스터링 성능이 떨어짐을 알 수 있다.
- The DBSCAN algorithm views clusters as areas of high density separated by areas of low density. Due to this rather generic view, clusters found by DBSCAN can be any shape, as opposed to k-means which assumes that clusters are convex shaped.
- The K-means algorithm aims to choose centroids that minimise the inertia, or within-cluster sum-of-squares criterion. Inertia can be recognized as a measure of how internally coherent clusters are. It suffers from various drawbacks: Inertia makes the assumption that clusters are convex and isotropic, which is not always the case. It responds poorly to elongated clusters, or manifolds with irregular shapes. -> k-means의 한계점

DBSCAN 알고리즘
DBSCAN은 클러스터를 저밀도 부분들에 의해 구분되어지는 고밀도 부분이라고 본다. 클러스터를 convex 형태라고 가정하는 k-means와 달리 DBSCAN에 의해 구분되어지는 클러스터들은 어떠한 모양이라도 될 수 있다.
DBSCAN의 주요 하이퍼파라미터에는 다음 두 가지가 있다. min_sampls가 높고 eps가 낮을수록 클러스터를 형성하는데에 더 높은 밀도가 요구된다.
- eps: 두 점을 이웃이라고 볼 수 있는 최대 거리. 두 점 사이의 거리가 eps 이하일 때 이웃으로 간주한다
- 가장 중요한 하이퍼파라미터. 데이터셋과 설정한 거리 계산 메트릭에 적절하게 설정해야 한다.
- 너무 작으면 생성되는 클러스터의 수가 많아지고, 비교적 sparse한 클러스터는 노이즈로 분류된다. (노이즈 수 증가) 너무 크면 비교적 dense한 가까운 클러스터들이 하나로 뭉쳐질 수 있다. 이는 데이터 내에 밀도가 다른 클러스터들이 많을수록 클러스터링이 하나의 eps 값으로 충분하지 않음을 나타낸다. 따라서 DBSCAN은 데이터 내의 밀도 차이가 클수록 eps 값에 영향을 많이 받는다. - min_samples: Core point가 되기 위해 eps 반경 내에 있어야 하는 점의 최소 개수(자기 자신 포함). 클러스터를 형성하려면 min_samples개 이상의 점이 클러스터 내에 있어야 한다.
- 알고리즘이 이상치에 얼마나 tolerant 한지를 제어한다. noisy하고 큰 데이터셋일수록 크게 설정하는게 좋다.
- 너무 작으면 이상치로 분류되어야 할 점들도 Core point나 Border point로 분류되고 클러스터의 수가 많아진다.
eps와 min_samples를 결정하는 방법에 대해서는 아래에서 더 설명할 예정이다.
DBSCAN에 의해 데이터는 Core point, Border point, Outliers로 구분된다.
- Core point (핵심 포인트): eps 반경 내에 자기 자신 포함 min_samples개 이상의 점들이 있으면 Core point가 된다. (Core point와 Border point가 모여 클러스터가 됨)
- Border point (경계 지점): 주변 Core point에서 eps 내에 도달할 수 있어 클러스터에는 속하지만, 반경 내에 min_samples개 이상의 점들이 있지 않아 Core point가 될 수 없는 경우이다. 주로 클러스터의 외곽을 이루는 점이 된다.
- Outliers (Noise, 이상치): 어느 클러스터에도 속하지 않는, Core point도 Border point도 아닌 점. 그 어떤 point에서도 도달할 수 없을 때 이상치로 분류
더보기 클릭
More formally, we define a core sample as being a sample in the dataset such that there exist min_samples other samples within a distance of eps, which are defined as neighbors of the core sample. This tells us that the core sample is in a dense area of the vector space. A cluster is a set of core samples that can be built by recursively taking a core sample, finding all of its neighbors that are core samples, finding all of their neighbors that are core samples, and so on. A cluster also has a set of non-core samples, which are samples that are neighbors of a core sample in the cluster but are not themselves core samples. Intuitively, these samples are on the fringes of a cluster.
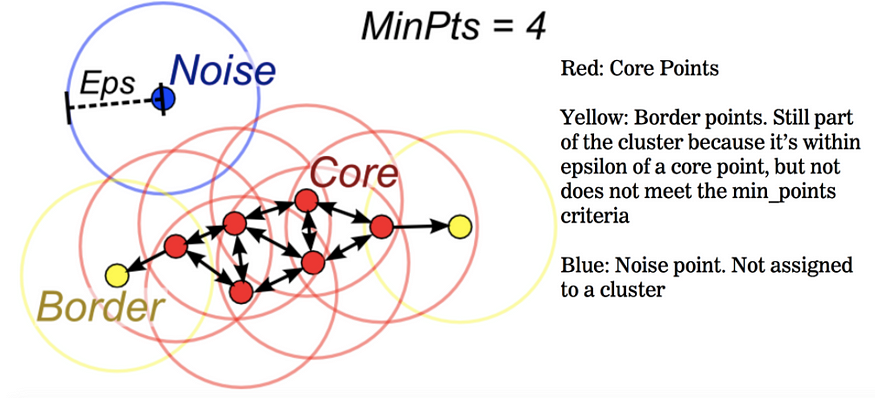

DBSCAN의 작동방식은 아래와 같다.
- Step 1: 데이터가 붐비는 밀집지역을 찾아 시작점을 무작위로 선택한다.
- Step 2: 시작점의 eps 반경 내에 min_samples개 이상의 점이 있으면 해당 포인트가 Core point로 정의된다. 정의한 Core point의 이웃들이 다시 반경 내에 min_samples개 이상의 점을 가진다면 Core point들로 정의하거나 방문한다.
- Step 3: 정의한 각 Core point가 클러스터에 포함되어 있지 않은 상태라면 새로운 클러스터를 생성한다. 각 Core point의 이웃들을 찾아 Core point와 같은 클러스터에 할당한다.
- Step 4: 모든 포인트들을 방문할 때까지 반복한다. 반복이 끝나고 그 어떤 클러스터에도 속해있지 않은 점들이 Outlier가 된다.




DBSCAN의 하이퍼파라미터(eps, min_samples)를 결정하는 Heuristic method
*Heuristic method: 불충분한 시간이나 정보로 인하여 합리적인 판단을 할 수 없거나, 체계적이면서 합리적인 판단이 굳이 필요하지 않은 상황에서 사람들이 빠르게 사용할 수 있는 어림짐작의 방법
아래와 같은 방법으로 데이터에서 가장 밀도가 낮은(가장 적은 포인트를 갖는) 클러스터를 잘 클러스터링할 수 있는 eps와 min_samples를 알아내어 DBSCAN의 하이퍼파라미터로 설정할 수 있다.
1. min_samples 결정 방법: ln(n) (n: 전체 데이터 포인트(관측치) 개수)
결정하는데에 Domain knowledge를 반영할 필요가 있지만 불가능한 경우 2차원 데이터에서는 min_samples = 4로, 3차원 이상에서는 min_samples = 2 * dimension으로 설정할 것을 권장한다. 데이터마다 구조나 데이터 개수(n)가 다를 수 있다는 점을 고려해서 min_samples = ln(n)으로 설정할 수도 있다. (min_samples ≥ dimension + 1 이어야 한다.)
2. eps 결정 방법: sorted K-distance graph를 그려서 Elbow(Knee) method 적용
sorted K-dist graph를 그린 후 Elbow(Knee) method를 적용해 경사가 급격하게 바뀌는 지점(Elbow or Knee)의 distance(y축 값)를 eps로 결정한다.
sorted K-dist graph를 그리기 위해서는 min_samples값이 먼저 결정되어 있어야 한다. min_samples = k라고 했을 때 데이터셋의 각 모든 점으로부터 k개의 가장 가까운 이웃들과의 거리를 구하고(k-Nearest Neighbors 사용), k번째로 가까운 점들과의 거리만 뽑아 오름차순으로 정렬한다(ex. sorted(distances[:, k-1])). 정렬된 array로 K-dist graph를 그리면 x축은 데이터셋의 모든 포인트들이 정렬되어 나타난 것이 되고, y축은 해당 포인트와 k번째로 가까운 점과의 거리가 된다. (즉, 데이터셋의 각 모든 포인트들과 k번째로 가까운 점들과의 거리를 오름차순으로 나타낸 것)
(구글링해보니 데이터 포인트와 가장 가까운 모든 k개의 이웃들과의 거리를 평균내어 K-dist graph를 그리는 방법도 있다. 즉, k번째 이웃과의 거리만으로 그리는 것이 아니라 k개 이웃들과의 각 거리의 평균으로 그리는 것)
threshold point의 왼쪽은 클러스터, 오른쪽은 노이즈로 구분된다. 결국 threshold point 이하의 점들은 모두 Core point가 되는데, graph의 의미를 생각해보면 threshold point 이하의 점들은 모두 eps반경 내에 min_samples개(k개) 점을 충족하기 때문이다. (graph는 k번째 점들로 그려진 것이기 때문) 반면 threshold point 오른쪽의 점들은 k번째 포인트가 모두 eps 초과의 거리에 있기 때문에 반경 내에 min_samples개 점을 충족하지 않아 노이즈가 된다.

DBSCAN의 장점
- k-means와 같이 미리 클러스터의 수를 정할 필요가 없다.
- 밀도에 따라 클러스터를 서로 연결하기 때문에 기하학적인 모양을 갖는 클러스터도 잘 찾을 수 있다. (DBSCAN supports non-globular structures as well)
- low density 클러스터로부터 high density 클러스터를 잘 분리해낸다.
- Noise points를 통해 이상치 탐색이 가능하다. (이상치에 robust 하다)
- 느리지만 비교적 큰 데이터셋에도 적용 가능하다
DBSCAN의 단점
- 알고리즘을 시행할 때마다 데이터 order가 달라지면 매번 1) 클러스터의 레이블 또한 달라지고, 2) Border point들이 속하게 되는 클러스터도 달라진다.
서로 다른 클러스터에 속해 있는 하나 이상의 Core point에서 도달할 수 있는 Border point는 결국 하나 이상의 클러스터에 속해질 수 있다는 것이고, 포인트들을 순회하는 순서에 따라 어떤 클러스터에 속해지는지가 달라지기 때문이다. (삼각부등식에 의해 해당 Core point들은 eps보다 멀리 떨어져있어야 함. 그렇지 않으면 같은 클러스터에 속해 있는 것이기 때문) 여기서 Border point는 먼저 생성된 클러스터에 속하게 된다. (같은 데이터를 같은 order로 시행하는 경우엔 항상 동일하게 클러스터링함)
The DBSCAN algorithm is deterministic, always generating the same clusters when given the same data in the same order. However, the results can differ when data is provided in a different order. - 고차원 데이터셋에서 eps 하이퍼파라미터를 정하기가 어려워진다.
Scikit-learn 공식문서
- [scikit-learn DBSCAN 공식문서]
- [scikit-learn 2.3. Clustering 공식문서]
- [scikit-learn 2.3. Clustering - DBSCAN 공식문서]
- [scikit-learn DEMO of DBSCAN clustering algorithm 공식문서]
Reference
1. Outlier(이상치/이상값/특이값/특이치 등) 탐지 방법(detection method) : 4. DBSCAN 방식 with 파이썬
3. 데이터 이상치(Outlier)의 기준은 무엇일까?
4. [ML with Python] 3. 비지도 학습 알고리즘 DBSCAN
5. DBSCAN Algorithm for Fraud Detection & Outlier Detection in a Data set
6. 클러스터링 #3 - DBSCAN (밀도 기반 클러스터링)
7. Let's cluster data points using DBSCAN
8 A routine to choose eps and minPts for DBSCAN
9. [R] 밀도 기반 군집분석 DBSCAN 의 입력 모수 Eps, MinPts 결정 방법 (Determining the Parameters Eps and MinPts) ⭐
10. [논문] DBSCAN 리뷰 : Density Based Spatial Clustering of Applications with Noise ⭐
11. [머신러닝] 클러스터링 평가지표 - 실루엣 계수 (1)
12. DBSCAN: Density-Based Clustering Essentials ⭐
13. [Kaggle] NearestNeighbors to find optimal 'eps' in DBSCAN -> 코드셀 [8] 부분의 코드가 잘못 되어있음. 수정된 코드는 내 코드 참고
14. [Kaggle] Outlier Detection Techniques: Simplified
15. Outlier detection methods!
16. [머신러닝] 클러스터링 평가지표 - 실루엣 계수 (2)
'Data Science' 카테고리의 다른 글
| [이상치 탐색] 2. ML을 통한 Outlier Detection - (3) Extended Isolation Forest (EIF) (0) | 2023.05.10 |
|---|---|
| [이상치 탐색] 2. ML을 통한 Outlier Detection - (2) Isolation Forest (with scikit-learn) (0) | 2023.05.04 |
| [이상치 탐색] 1. 통계값을 이용한 Outlier Detection (0) | 2023.05.03 |
| 클러스터링 평가지표 - 실루엣 계수 (0) | 2023.05.02 |
| 이상치를 무작정 제거하면 안되는 이유 | Why You Shouldn’t Just Delete Outliers (0) | 2023.04.06 |



