Studying data
[이상치 탐색] 2. ML을 통한 Outlier Detection - (2) Isolation Forest (with scikit-learn) 본문
[이상치 탐색] 2. ML을 통한 Outlier Detection - (2) Isolation Forest (with scikit-learn)
halloweenie 2023. 5. 4. 00:03Isolation Forest
• 결정 트리에서의 이상치 분리
• Anomaly score
• IsolationForest 알고리즘
- 하이퍼파라미터
- Attributes
- Methods
Isolation Forest
결정 트리(decision tree) 계열의 비지도 학습 알고리즘으로 고차원(high-dimensional) 데이터셋에서 이상치를 탐지할 때 효과적인 방법이다. (통계값을 사용한 이상치 탐색 방법인 IQR과 Z-score 방식은 고차원 데이터셋에서는 잘 사용하지 않는다고 한다.) IQR이나 Z-score 방식은 먼저 정상 데이터의 영역을 찾아낸 후 이외의 영역이 이상치인지를 판별하는 반면, Isoation Forest 방식은 전체 데이터에서 이상치를 분리해 찾아낸다. 이 알고리즘은 이상치는 소수이며, 일반적인 데이터값과 매우 다른 속성을 가진다는 특성을 활용한다.
… our proposed method takes advantage of two anomalies’ quantitative properties: i) they are the minority consisting of fewer instances and ii) they have attribute-values that are very different from those of normal instances. - Isolation Forest, 2008
결정 트리에서의 이상치 분리
Isolation Forest는 여러개의 binary (isolation) trees를 사용하여 이상치를 탐색한다. 먼저 데이터셋을 결정 트리 형태로 표현하게 되는데, 각 노드에서 데이터를 분리하는 데에 쓰일 특성과 split value를 랜덤하게 선택해 i)리프 노드에 하나의 샘플만 남거나 같은 값의 샘플들만 남을 때까지 또는 ii)트리의 *최대 깊이에 도달할 때까지 트리를 아래로 뻗어나간다. 샘플이 split value보다 작으면 왼쪽 branch를 따라 내려가고, 그렇지 않으면 오른쪽 branch를 따라 내려간다.
*최대 깊이에 대해서는 아래에서 설명할 예정


이상치는 트리의 상단에서 일찍 분리되고, 반대로 정상 데이터 값의 경우 상대적으로 트리의 깊이가 깊어져야 분리된다. 즉, 데이터를 partitioning 해나가면 전체에서 이상치를 먼저 분리하는 편이 더 쉽다는 것이다.

(a)는 Isolation Forest에 있는 하나의 트리를 표현한 것인데 빨간 선은 루트 노드로부터 이상치가 있는 노드까지의 경로이고, 파란 선은 루트 노드로부터 정상치가 있는 노드까지의 경로이다. 여기서도 이상치는 비교적 빨리 분리된 반면, 정상치는 트리의 최대 깊이까지 내려간 것을 볼 수 있다.
(b)는 Isolation Forest 전체를 나타낸 그림이다. 각 라인은 트리 한개를 뜻하며 총 60개의 트리가 있는 forest이다. 가장 바깥쪽의 원은 트리의 최대 깊이를 나타낸다. 마찬가지로 빨간 선과 파란 선은 각각 하나의 트리에서 이상치와 정상치의 경로 길이를 의미한다. 파란 선이 평균적으로 반경이 더 긴 것을 확인할 수 있다.
아래는 정상치와 이상치 각각의 branching(partitioning) process를 나타낸 그림이다. 위에서 설명한 바와 같이 이상치/정상치가 하나의 파티션 안에 분리되거나(isolated), 트리의 최대 깊이에 도달할 때까지 branching이 계속된다. (샘플이 완전히 분리되기 전에 최대 깊이에 도달하면 branching을 중단한다.)
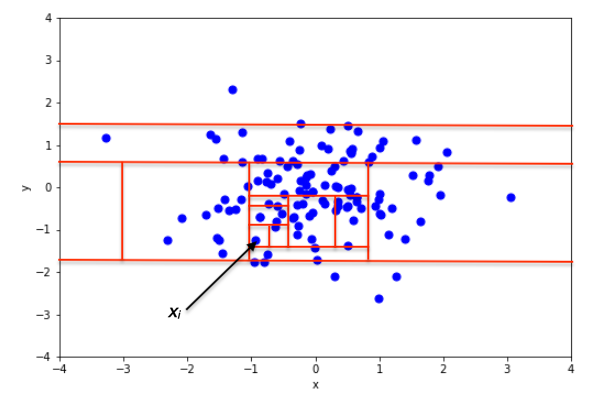


위 그림들에서처럼 이상치는 항상 정상치들로부터 멀리 떨어져 있기 때문에 적은 횟수의 랜덤한 파티션 분할로도 쉽게 분리가 가능하게 된다. 이를 결정 트리의 관점에서 보자면 이상치는 적은 횟수의 랜덤 split으로 쉽게 isolate되기 때문에 루트 노드로부터 가깝게 위치하게 되는 것이다.
위 branching process를 나타낸 그림들과 아래 그림에서 선(random branch cuts)들은 모두 수직이거나 수평인데 그 이유는 분리 기준(branching criteria)인 특성과 split value를 정할 때 랜덤으로 한번에 하나의 특성, 값만을 선택하기 때문이다.
트리를 만들 때 우리는 아래로 branch를 뻗어내려가고, 그 과정에서 데이터가 분리되기 때문에 선택 가능한 split value의 범위는 점점 줄어들게 된다. (e.g. 위 그림의 (b)에서 빨간 점인 정상치를 분리해낼 때 0번과 1번 partition을 긋고 나면 x축 특성에서 가능한 split value 범위는 약 -1~1.2 사이로 줄어든다.) 결과적으로 branch cut들은 데이터 포인트들이 가장 많이 모여있는 지역에 밀집하게 된다.
random branch cuts가 수평 또는 수직일수밖에 없다는 특징은 Isolation Forest의 anomaly score map에서 발견되는 문제의 원인이 되는데, 이에 대해서는 다음 글에서 해결책인 Extended Isolation Forest와 함께 더 자세히 설명할 예정이다.

Anomaly score
각 트리의 샘플이 있는 리프 노드에서 루트 노드까지의 경로가 짧을수록 anomaly score가 높아지도록 score를 설정하여, anomaly score가 높을수록 이상치라고 판단한다. anomaly score의 공식은 다음과 같다.

\(h(x)\)는 하나의 트리 내에서 루트 노드로부터 해당 샘플 \(x\)가 있는 노드까지 경로의 길이이고, \(E(h(x))\)는 샘플에 \(x\)에 대해 모든 트리에서 나온 경로의 길이를 평균낸 것이다. \(c(n)\)은 \(E(h(x))\)를 보정해주기 위한 정규화 인자로 이진탐색트리에서 성공하지 못한 탐색의 평균 깊이이다. \(n\)은 하나의 트리를 만드는 데에 쓰인 샘플의 개수이다.
$$c(n) = 2H(n-1) - (2(n-1)/n)$$
$$H(i) = ln(i) + 0.5772156649 (Euler's constant)$$
결과로 나온 anomaly score는 0~1 사이의 값이 된다.
- 1에 가까울수록 이상치
- 0.5보다 훨씬 작은 경우 정상 관측값으로 판별
- 모든 관측값의 score가 0.5에 가까우면 전체 데이터셋에서 명확하게 구별되는 이상치가 없는 것으로 본다.
*리프 노드에서 루트 노드까지의 경로(depth of the leaf) = the number of splits
IsolationForest 알고리즘
IsolationForest는 ExtraTreeRegressor의 앙상블에 기반한 모델이다.
앙상블 기법은 하나의 데이터에서 만든 여러 sub-sample들로 여러개의 머신러닝 기본모델(base estimators, weak base learner)을 학습시켜 나온 예측 결과를 다수결이나 평균을 내 최종 예측하는 방법이다.
IsolationForest는 위에서 설명한 랜덤한 결정 트리를 기본모델로 하여 여러개를 만든다. 그리고 각 결정 트리에서 루트 노드로부터 해당 샘플이 있는 리프 노드까지의 거리(depth)를 사용해 샘플마다의 anomaly score를 구하고, 각 트리들에서 해당 샘플에 대해 얻은 모든 anomaly score를 평균낸다. 마지막으로 이 average anomaly score를 통해 해당 샘플이 이상치인지 아닌지를 판별하게 된다.
여기서 각 트리에서 구한 anomaly score들을 평균내는 이유는, 랜덤하게 생성된 트리들이 어떤 특정 샘플에 대해 계속해서 모두 비교적 짧은 depth를 보인다면 그 샘플이 이상치일 가능성이 다분해지기 때문이다.
Random partitioning produces noticeably shorter paths for anomalies. Hence, when a forest of random trees collectively produce shorter path lengths for particular samples, they are highly likely to be anomalies. - scikit-learn 2.7.3.2. Isolation Forest

• 각 트리에 사용하는 데이터는 원본 데이터에서 랜덤으로 샘플링을 하게 되는데 이때 하이퍼파라미터 bootstrap을 True로 설정하면 부트스트랩(Bootstrap) 샘플링을 진행한다. (Bootstrap 샘플링이란 Sampling with replacement, 즉 복원추출하는 것을 말한다.) IsolationForest 모델의 하이퍼파라미터에 대해서는 뒤에서 더 설명할 예정이다.
• IsolationForest는 결정 트리를 만드는 과정에서 각 노드에서 데이터를 분류할 때 쓰일 i)특성(feature)을 랜덤하게 선택하고, ii)분류 기준값(split value) 또한 최소, 최대값 범위 사이에서 랜덤하게 선택해 샘플을 분리해나간다.
• Isolation Forest 논문에 따라 각 트리의 최대 깊이는 \(log_2(n)\)의 올림으로 설정되며, 여기서 \(n\)은 트리를 만드는데 쓰인 샘플의 개수이다. 대략적으로 평균 트리 깊이와 일치한다. 트리를 평균 트리 깊이까지만 제한하여 생성하는 이유는 평균 트리 깊이보다 깊이(경로의 길이)가 작은 노드들이 이상치일 확률이 높기 때문이다.
Algorithm 1과 2는 Training stage, Algorithm 3은 Evaluating stage에 해당한다.
[Training Stage]

- sub-sampling size \(\psi\)는 적절한 값으로 설정하면 안정적으로 이상치 탐지를 할 수 있으며, 최적의 값을 넘어서면 시간과 메모리 낭비가 될 수 있기 때문에 그 이상으로 값을 올릴 필요는 없다. 원 논문에서는 256으로 설정했을 때 충분한 성능을 보였다고 한다.
- number of trees \(t\)는 원 논문의 경우 \(t\)=100 이전에 경로의 길이가 수렴했다고 한다.

Algorithm 1과 2를 실행하고 나면 학습된 트리 세트가 반환되어 Evaluating stage로 들어가게 된다.
[Evaluating Stage]

Evaluating stage에서는 Algorithm 3을 통해 계산된 각 샘플의 path length (\(h(x)\))로 anomaly score를 계산한다.
- 샘플이 리프 노드에 도달하면 \(e\)에 조정값인 \(c(T.size)\)를 더한 값을 반환한다. \(c(T.size)\)는 트리의 최대 깊이를 넘어서 만들어질 수 있었던 unbuilt subtree를 의미하며 위 anomaly score 부분에서 설명한 \(c(n)\) 공식으로 계산한다.
- 샘플이 split value보다 작으면 왼쪽 branch로, 크거나 같으면 오른쪽 branch로 내려간다.
- 최종적으로 \(PathLength()\)를 통해 각 트리에서 \(h(x)\)를 계산했으면, \(h(x)\)를 사용하여 anomaly score를 구한다.
하이퍼파라미터
• n_estimators: 앙상블에 쓰일 기본 모델의 개수. 즉, 결정 트리의 개수
• max_samples: 원 데이터셋에서 샘플링하여 각 결정 트리를 학습시키는데에 쓰일 샘플의 개수 (주어진 데이터셋의 샘플수보다 더 크게 설정되면 그냥 전체 데이터셋을 학습에 사용한다. 샘플링하지 않음)
• contamination: 데이터셋의 오염도. 즉, 데이터셋에서 이상치의 비율을 뜻한다. offset_ 값을 좌우한다. "auto"로 설정하면 논문대로 0.1이 되고, 직접 설정하는 경우 0 초과 0.5 이하의 값이어야 한다. 실제로 모델 예측 결과를 보면 [전체 샘플수*contamination]개(올림하여)의 샘플을 이상치로 판별한다.
• max_features: 결정 트리 학습에 사용할 특성의 개수. 데이터셋의 전체 특성 수보다 적게 설정되는 경우 feature subsampling을 진행하므로 시간이 더 오래걸릴 수 있다.
• bootstrap: 결정 트리 학습에 쓰일 데이터를 샘플링할 때 bootstrap=True이면 복원추출(sampling with replacement), False이면 비복원추출(sampling without replacement) 진행
• warm_start: True면 이미 학습된 앙상블 모델에 기본 모델을 추가한다. False이면 전체 forest를 처음부터 다시 학습시킨다.
# Add more estimators(trees) to an already fitted ensemble model by setting warm_start=True
X = np.array([[-1, -1], [-2, -1], [-3, -2], [0, 0], [-20, 50], [3, 5]])
clf = IsolationForest(n_estimators=10, warm_start=True)
clf.fit(X) # fit 10 trees
clf.set_params(n_estimators=20) # add 10 more trees
clf.fit(X) # fit the added trees
Attributes
• estimator_: 앙상블에 사용된 기본 모델의 정보 반환

• estimators_: 모든 기본 모델들의 정보 반환
e.g.

• estimators_features_: 각 기본 모델의 학습에 사용한 특성들의 이름 반환
• estimators_samples_: 각 기본 모델의 학습에 사용한 샘플들(in-bag samples)의 인덱스 반환
*학습에 사용되지 않은 샘플들은 out-of-bag(OOB) samples라고 한다.
• max_samples_: 각 기본 모델의 학습에 사용된 샘플의 개수 (e.g. 위 코드의 모델의 경우 256 반환)
• offset_: score_samples() 메소드로 확인할 수 있는 mean anomaly score로부터 decision function(decision_function() 메소드로 반환 가능)을 계산하는 데에 쓰인다. 샘플의 decision_function 값이 음수이면 이상치로 판별한다. 공식은 다음과 같다.
decision_function = score_samples - offset_
contamination 하이퍼파라미터가 "auto"이면 offset_ 값은 -0.5로 딱 떨어지게 설정된다. 정상치(inliners)의 score_samples는 0에 가깝고, 이상치의 score_samples는 -1에 가깝게 나오기 때문이다. 따라서 score_samples가 -0.5 이상이면 정상치, 미만이면 이상치가 되고, offset_을 빼 계산한 decision_function이 음수인 샘플들이 이상치가 된다.
(e.g. 정상치의 score_samples: -0.48, 이상치의 score_samples: -0.54 => 정상치의 decision_function: 0.02(≥0), 이상치의 decision_function: -0.04(<0))
contamination이 "auto" 이외의 값으로 설정되어 있으면 decision_function < 0인 샘플들이 설정된 이상치의 개수에 맞게 나오도록 offset_ 값이 자동으로 설정된다.
Methods
• decision_function(X): 각 샘플들의 average anomaly score를 반환하는데, score_samples()에서 offset_을 뺀 값이다. 낮을수록 더 abnormal함을 뜻하며, 음수인 경우 이상치로 판별한다. (실제로 예측해보면 decision_function()으로 반환한 값이 음수인 샘플들의 레이블이 -1(이상치 레이블)로 나온다.)
• fit_predict(X, y=None): 모델 학습 후, 각 샘플에 대해 예측한 이상치 레이블 반환. -1이면 이상치, 1이면 정상치이다.
• score_samples(X): 각 샘플들의 average anomaly score 반환(*score가 원 논문과 반대라고 한다.). 낮을수록 더 abnormal함을 의미한다. score_samples()에서 offset_을 빼 decision_function()을 구한다.
*When a forest of random trees collectively produce short path lengths for isolating some particular samples, they are highly likely to be anomalies and the measure of normality is close to 0. Similarly, large paths correspond to values close to 1 and are more likely to be inliers. - scikit-learn IsolationForest example
이 부분을 의미하는 것 같다(?) 해석해보면 scikit-learn IsolationForest 알고리즘의 measure of normality는 0에 가까울수록 이상치, 1에 가까울수록 정상치이다. (원 논문에서는 1에 가까울수록 이상치)

위 그림을 보면 decision boundary가 등고선처럼 방사상이 아님을 확인할 수 있는데, 이는 클러스터의 중앙으로부터 같은 거리에 있는 포인트들이라도 이상치 또는 정상치로 서로 다르게 판별될 수 있기 때문에 문제가 된다. 이러한 Isolation Forest의 문제점에 대해서는 다음 글에서 더 robust한 알고리즘인 Extended Isolation Forest와 함께 다뤄볼 예정이다.
Scikit-learn 공식문서
- [scikit-learn IsolationForest 공식문서]
- [scikit-learn 2.7. Novelty and Outlier Detection - Isolation Forest 공식문서]
- [scikit-learn IsolationForest example 공식문서]
- Comparing anomaly detection algorithms for outlier detection on toy datasets
Isolation Forest paper
Reference
1. Outlier(이상치/이상값/특이값/특이치 등) 탐지 방법(detection method) : 3. Isolation Forest 방식 with 파이썬
3. 데이터 이상치(Outlier)의 기준은 무엇일까?
4. Outlier Detection with Isolation Forest
6. 4 Automatic Outlier Detection Algorithms in Python
8. [Kaggle] Outlier Detection Techniques: Simplified
10. Evaluation of outlier detection estimators -> LOF와 IsolationForest 모델 성능 평가
11. Anomaly detection using Isolation Forest - A Complete Guide
12. Isolation Forest from Scratch
'Data Science' 카테고리의 다른 글
| [이상치 탐색] 2. ML을 통한 Outlier Detection - (4) Mahalanobis Distance (with scikit-learn) (0) | 2023.05.21 |
|---|---|
| [이상치 탐색] 2. ML을 통한 Outlier Detection - (3) Extended Isolation Forest (EIF) (0) | 2023.05.10 |
| [이상치 탐색] 1. 통계값을 이용한 Outlier Detection (0) | 2023.05.03 |
| 클러스터링 평가지표 - 실루엣 계수 (0) | 2023.05.02 |
| [이상치 탐색] 2. ML을 통한 Outlier Detection - (1) DBSCAN (with scikit-learn) (0) | 2023.04.29 |



