Studying data
[이상치 탐색] 2. ML을 통한 Outlier Detection - (3) Extended Isolation Forest (EIF) 본문
[이상치 탐색] 2. ML을 통한 Outlier Detection - (3) Extended Isolation Forest (EIF)
halloweenie 2023. 5. 10. 17:31• Isolation Forest의 문제점
• Extended Isolation Forest (EIF)
- EIF의 branch cuts
- EIF의 Extension Levels
- EIF 알고리즘
- EIF의 anomaly score map
Isolation Forest의 문제점

위 그림은 2차원 정규 분포에서 샘플링된 (a)데이터와 해당 데이터에 대해 Isolation Forest로 생성된 (b)anomaly score map이다. 논문에 따르면 anomaly score map에서 색이 어두울수록 높은 anomaly score, 즉 더 anomalous함을 뜻한다.
왼쪽 그림을 보면 직감적으로 각 샘플의 anomaly score가 중앙의 점부터 바깥쪽으로 갈수록 방사상으로 높아져 anomaly score map이 전체적으로 등고선처럼 원형으로 나타날 것이라 예측할 수 있다. 즉, 클러스터의 중앙으로 부터 같은 거리에 있는 샘플들은 같은 anomaly score일 것이라 추측할 수 있다. 그러나 (b)를 보면 anomaly score의 변화가 방사상이지 않음이 보인다. 또, 4사분면의 경계쪽을 보면 낮은 anomaly score 범위가 수직, 그리고 수평으로 여러개 나타나있다. 논문에서는 이를 "artifacts"라 칭한다.
여기서 Isolation Forest의 문제는 이 artifacts에 의해 서로 다른 샘플들이 클러스터의 중앙으로부터 같은 거리에 있더라도 anomaly score가 달라져 각각 정상치와 이상치로 다르게 판별될 수 있다는 것인데, 이러한 경우 알고리즘에 대한 신뢰도는 떨어지게 된다. 또한 anomaly score에 기반하여 데이터의 분포에 대해 확률 밀도 함수를 얻고 싶을 때 (b)와 같이 anomaly score 분포의 표현이 명확하지 않다면 문제가 된다.

이번에는 두 개의 클러스터가 각각 [0, 10]과 [10, 0] 위치를 중심으로 형성되어 있는 데이터이다. (b)anomaly score map에서는 artifacts 뿐만 아니라 [0, 0]과 [10, 10] 위치에 "ghost 클러스터"가 보인다. Isolation Forest는 이 ghost 클러스터 부근에 위치한 이상치들의 anomaly score를 낮게 보고 정상치로 판별할 것이기 때문에 문제가 된다. 즉, anomaly score map의 오류는 이상치를 정상치로 판별할 확률을 높이고, 데이터에 존재하지 않는 어떤 구조(ghost 클러스터)가 존재한다고 보기 때문에 문제가 된다.

세번째 예시의 경우, 데이터는 사인파의 peak 부분에 가우시안 노이즈가 첨가된 양상을 띤다. robust한 알고리즘이라면 anomaly score map에서 이 데이터의 사인파 형태를 발견해내야 하지만 (b)를 보면 잘 작동하지 않았음을 확인할 수 있다. (b)에서 알고리즘은 사인파 형태를 찾아내기 보다는 데이터를 하나의 큰 직사각형과 각 축에 수평인 artifacts의 형태로 보고 있다. 만약 위로 솟아있는 두 hills 사이에 이상치가 존재하더라도 Isolation Forest는 해당 이상치의 anomaly score를 낮게 보고 정상치로 분류할 것이다. ((b)anomaly score map을 보면 두 hills 사이를 낮은 anomaly score 구간으로 뭉쳐버렸기 때문)
이렇게 Isolation Forest의 anomaly score map에 artifacts가 나타나는 이유는 이전 글에서도 설명했듯이 branch cuts가 수직 또는 수평의 형태만을 띠기 때문이다. branch cuts가 수직 또는 수평의 형태만 띠는 것은 branching(partitioning) process에서 한번에 하나의 랜덤한 decision boundary(i.e. branching criteria)가 선택되기 때문이다. (한번에 하나의 랜덤한 특성과 그 특성의 최대 최소값 내에서 랜덤 split value를 선택 → x축에 수직 또는 y축에 수직으로 나타남) 또, *데이터가 집중되어 있는 지점에 branch cuts 선들이 밀집하게 된다고 설명했었는데, 문제는 선이 모두 수평 또는 수직이기 때문에 데이터 포인트가 많지 않은 지역에도 많은 branch cuts들이 몰리게 된다는 것이다.
* 데이터 포인트가 집중되어 있는 곳에서는 하나의 포인트를 분리하기 위해 파티션이 많이 필요하기 때문에 branch cuts가 밀집되는게 당연. 반대로 데이터 포인트 미집중 지역에서는 하나의 포인트 분리에 파티션이 적게 필요하기 때문에 branch cuts가 sparse하게 나타남.
+데이터를 분리(branching)해나가면서 가능한 split value 범위가 점점 줄어들기 때문이기도 함


바로 위 (a)들에서 [4, 0] 가까이에 위치한 포인트는 [3, 3] 근처에 위치한 포인트보다 훨씬 더 많은 branch cuts의 영향을 받게 된다. [3, 3] 근처의 포인트는 육안으로도 branch cuts가 적다. *어떤 지역에서의 branch cuts의 개수(밀도)는 그 지역의 anomaly score와 직결되기 때문에 결과적으로 두 포인트 모두 이상치임에도 불구하고 anomaly score는 매우 달라지게 된다. (anomaly score: [4, 0] < [3, 3])
* 포인트가 클러스터의 중앙에 있을수록(anomalous 하지 않을수록) 분리하는 데에 많은 branch cuts가 필요 → branch cuts가 dense할수록 낮은 anomaly score
이상치 분리는 적은 수의 branch cuts만으로도 가능 → branch cuts가 sparse할수록 높은 anomaly score
(c)에서는 y축의 특성에서 중복되는 값을 가지는 데이터가 많아 y축에 수직인 branch cuts는 약 -1.5~1.4 사이에만 매우 biased되어 나타나게 된다. 결과적으로 데이터의 구조를 제대로 파악하지 못하게 되는데, 이는 Example 3 그림에서 (c)의 anomaly score map을 통해 확인할 수 있다.
마지막으로 정리하자면
- Isolation Forest는 branch cuts의 i)수직 또는 수평인 특성, ii)밀집되는 특성때문에 모델 학습 과정 중 데이터가 집중되어 있지 않은 지역에도 branch cuts가 밀집될 수 있다. (branch cuts bias와 anomaly score map에 artifacts가 생김)
- ⇒ 밀집된 random branch cuts = 해당 지역의 anomaly score가 낮음. 결국 데이터가 집중되어 있지 않은 부분(anomalous한 지역)도 anomaly score가 낮은 지역(normal한 지역)이 되어버림
- ⇒ 클러스터의 중앙으로부터 같은 거리에 있는 점들이라도 anomaly score가 달라져서 이상치/정상치 판별이 달라짐(거리에 따라 일관되지 않음)
더 정확하고 robust한 알고리즘을 위해서 이러한 이슈를 해결하는 것은 아주 중요하며, 이를 위해 나온 방법이 Extended Isolation Forest (EIF)이다.
Extented Isolation Forest (EIF)
Extended Isolation Forest의 branch cuts
Extended Isolation Forest (EIF)는 Isolation Forest의 문제를 해결하기 위해 branch cuts가 반드시 수평, 수직인 것이 아니라, 랜덤한 기울기를 갖도록 branching process를 수정한 방법이다.

Isolation Forest는 branch cuts를 설정할 때 랜덤한 i)특성의 랜덤한 ii)split value가 필요했다. Extended Isolation Forest의 경우에는 branch cuts 설정에 랜덤한 i)기울기와 랜덤한 ii)intercept(y절편)가 필요하다(e.g. \(y=ax+b\)). intercept는 학습 데이터의 가능한 값 범위 내에서 랜덤으로 선택된다. Isolation Forest에서와 마찬가지로 데이터 포인트가 완전히 분리되거나(isolated) 트리가 최대 깊이에 도달할 때까지 bracnching(partitioning)을 계속한다.
For an N dimensional dataset, selecting a random slope for the branch cut is the same as choosing a normal vector, \(\vec{n}\), uniformly over the unit N-Sphere. This can easily be accomplished by drawing a random number for each coordinate of \(\vec{n}\) from the standard normal distribution N(0, 1). This results in a uniform selection of points on the N-sphere. For the intercept, \(\vec{p}\), we simply draw from a uniform distribution over the range of values present at each branching point. Once these two pieces of information are determined, the branching criteria for the data splitting for a given point \(\vec{x}\) is as follows: - Extended Isolation Forest, 2020
$$(\vec{x}-\vec{p}) \cdot \vec{n} \le 0$$
- \(\vec{x}\): data sample(point)
- \(\vec{n}\): random slope
- \(\vec{p}\): random intercept
위 식을 만족하면 샘플 \(\vec{x}\)는 왼쪽 branch로 내려가고, 아닌 경우 오른쪽 branch로 내려간다.
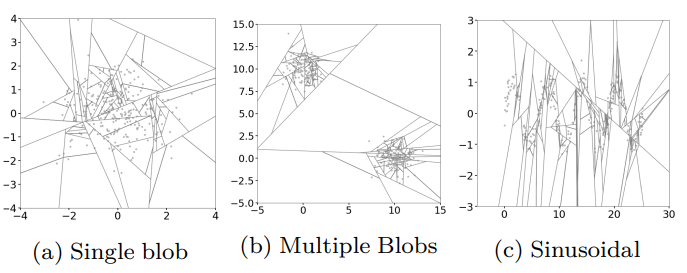

Extended Isolation Forest를 사용했을 때 클러스터들이 더 섬세하게 표현된 것을 확인할 수 있다.

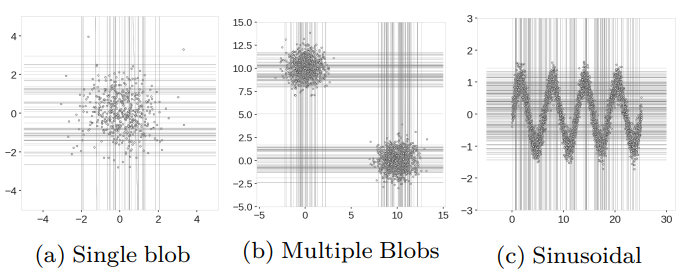
Extended Isolation Forest의 경우 좌표축에 상관없이 좌표평면의 모든 지역에서 branch cuts가 생성 가능한 것이 보인다. 반면 Isolation Forest는 branch cuts가 수직 또는 수평이어야 하므로 biased되어 나타난다.
데이터 밀집 지역에 branch cuts가 집중되는 현상은 여전히 나타나는데, 이는 트리가 깊어질수록 가능한 intercept \(\vec{p}\)의 범위가 점점 줄어들어 데이터가 존재하는 부분으로 서서히 accumulate되기 때문이다. 결과적으로, Isolation Forest에서와 마찬가지로 생성 가능한 branch cuts들은 데이터가 밀집된 지역에 모이는 경향이 생기고, 비교적 데이터가 sparse한 지역에는 생성 가능한 branch cuts 또한 sparse해진다.
그러나 Extended Isolation Forest는 Isolation Forest와 달리 데이터가 sparse한 부분에는 branch cuts가 집중되지 않아 anomaly score map에서 정상적으로 high anomaly score 지역으로 표시된다. (Isolation Forest는 (b)의 [0, 0], [10, 10] 부분과 같이 데이터가 sparse한 부분에도 branch cuts가 집중된다는 것이 문제였다.) 그 결과, Isolation Forest의 anomaly score map에서 보였던 low anomaly score의 artifacts, ghost 클러스터도 Extended Isolation Forest에서는 보이지 않게 되어 이상치를 이상치로 판별할 수 있게 된다.
Extended Isolated Forest의 Extension Levels
지금까지는 2차원 데이터의 직선 형태 branch cuts만 살펴보았지만 Extended Isolation Forest는 고차원 데이터에서도 잘 작동한다. 3차원 이상의 N차원 데이터는 N-1차원 hyperplane 형태의 branch cuts를 생성하게 된다. hyperplane 형태의 branch cuts를 생성할때도 랜덤한 기울기(\(\vec{n}\))와 intercept(\(\vec{p}\))를 결정하여 branching하는 과정은 똑같다.
N차원의 데이터셋으로는 0부터 N-1레벨의 extension까지 가능한데, fully extended된 경우인 N-1레벨의 branch cuts는 모든 축과 교차하게 되고, extension level이 1씩 줄어들수록 branch cuts와 교차하는 축이 하나씩 줄어든다(i.e. 평행인 축이 하나씩 늘어난다). 최저 extension인 0레벨 extension은 1개 축과 교차, N-1개의 축과 평행하게 되고, 이는 결국 standard Isolation Forest와 같다. (교차하는 축 = 데이터를 나누기 위한 random split value 설정에 쓰이는 특성)
예를 들어, 2차원 데이터셋의 1레벨 extension branch cuts는 x축, y축과 모두 교차하는 비스듬한 직선 형태가 된다(위 Figure1 참고). 0레벨 extension의 경우에는 1레벨에서 하나의 차원을 제외하게 되는 것으로, x축과 y축 중 하나의 축과 평행한 직선이 된다(x축에 수평 또는 y축에 수직). 즉, 0레벨 extension은 standard Isolation Forest인 것이나 마찬가지다(위 Figure2 참고).
3차원 데이터셋은 branch cuts가 2차원 평면형태인데, fully extended level인 \(2^{nd}\) Extension (Ex 2)에서 이 평면은 3개의 모든 축과 교차한다. \(1^{st}\) Extension (Ex 1)에서는 항상 셋 중 하나의 축과 평행하고, \(0^{th}\) Extension (Ex 0)은 항상 셋 중 두 개의 축과 평행하다(= standard IF).

extension level이 증가할수록 알고리즘의 bias는 감소한다. extension 커스텀은 다차원 데이터에서 각 dimension의 데이터 범위가 매우 다를 때 유용할 수 있다. 이런 경우, extension level을 줄이는 것이 최적의 branch cuts(split hyperplanes) 선택과 계산 오버헤드 감소에 도움이 될 수 있다. 예를 들어, 하나의 dimension의 cardinality가 다른 dimension들에 비해 낮은 경우, 해당 dimension을 selection bias를 줄이기 위해 무시할 수 있다. 또는 3차원 데이터에서 두 dimension의 데이터 범위가 다른 하나에 비해 훨씬 작은 경우, standard Isolation Forest (i.e. Extension Level=0)가 최적의 결과를 보일 것이다.
Extended Isolation Forest 알고리즘
[Training Stage]


Algorithm 1은 Isolation Forest와 같고, Algorithm 2는 4~9 라인이 Extended Isolation Forest에 맞게 수정되었다. 주목해야할 부분은 Extension Isolation Forest는 extension level을 조절할 수 있어서 라인 6가 추가된 것인데, extension level의 조절을 통해 이 알고리즘은 standard Isolation Forest로 쓰일 수도, Extended Isolation Forest로 쓰일 수도 있다. (실제로 iForest 모델에 ExtensionLevel 하이퍼파라미터가 있다. ExtensionLevel=0으로 설정하면 standard Isolation Forest로 작동한다.)
[Evaluating Stage]

Algorithm 3도 EIF에 맞게 branching criteria와 관련된 부분들이 수정되었다. IF와 마찬가지로 Evaluating stage에서는 PathLength()를 통해 각 트리에서 구한 path length (\(h(x)\))로 anomaly score를 계산하게 된다.
Extended Isolation Forest의 anomaly score map

Standard Isolation Forest와 비교하면 Extended Isolation Forest의 anomaly score map에서는 낮은 anomaly score의 artifacts가 더이상 드러나지 않고, anomaly score가 클러스터의 중앙으로부터 바깥쪽으로 갈수록 비교적 방사상으로 단조롭게 높아지고 있음이 보인다. 중앙으로부터 같은 거리에 있는 샘플들이 일관적으로 비슷한 anomaly score를 가지게 되며, 이상치를 이상치로 잘 판별할 수 있게 되었다.

두 개의 클러스터가 있는 데이터셋의 경우 Standard Isolation Forest에서는 branch cuts가 수직 또는 수평이어야 하는 성질 때문에 두 개의 ghost 클러스터와 artifacts가 나타나지만, Extended Isolation Forest에서는 완전히 사라진 것이 보인다. EIF의 map에서는 Standard IF에서는 찾아낼 수 없었던 구조가 보이는데, 두 개의 클러스터 사이에 연결시키는 것처럼 나타나는 higher anomaly score 구간이다(동그라미 친 부분). 이는 해당 구간이 다른 지역들보다 비교적 두 클러스터와 가깝지만 클러스터보다는 anomaly score가 높기 때문에 발견되는 구조이다.
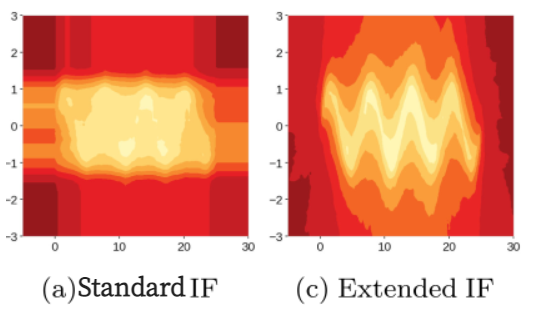
Standard IF는 데이터셋의 사인파 형태를 찾아내지 못하고 하나의 직사각형 모양으로 뭉뚱그려버린다. 반면 Extended IF는 데이터의 사인파 구조를 잘 보존하여 보여주고 있으며, artifacts 또한 사라졌다. 결과적으로 사인파의 두 hills 사이에 이상치가 존재하더라도 higher anomaly score 구간으로 잘 구분되어 있기 때문에 이상치로 잘 판별해 낼 수 있게 된다.
Extended Isolation Forest 논문
Extended Isolation Forest 라이브러리
Reference
1. Outlier Detection with Extended Isolation Forest
2. Extended Isolation Forest Example - Github code - Code from Reference 1.
3. https://medium.com/@dstanner/thanks-for-the-article-a-couple-of-points-questions-eb9ec8b7bc60 - response to Reference 1. (about some mistakes in the post)
4. https://medium.com/@ernstoldenhof/thanks-for-the-article-and-nice-explanations-ce507ffce17a - response to Reference 1. and github code link comparing IF and EIF algorithms by using AUC and Average Precision
'Data Science' 카테고리의 다른 글
| [이상치 탐색] 2. ML을 통한 Outlier Detection - (5) LOF(Local Outlier Factor) (with scikit-learn) (2) | 2023.05.29 |
|---|---|
| [이상치 탐색] 2. ML을 통한 Outlier Detection - (4) Mahalanobis Distance (with scikit-learn) (0) | 2023.05.21 |
| [이상치 탐색] 2. ML을 통한 Outlier Detection - (2) Isolation Forest (with scikit-learn) (0) | 2023.05.04 |
| [이상치 탐색] 1. 통계값을 이용한 Outlier Detection (0) | 2023.05.03 |
| 클러스터링 평가지표 - 실루엣 계수 (0) | 2023.05.02 |




