[이상치 탐색] 2. ML을 통한 Outlier Detection - (5) LOF(Local Outlier Factor) (with scikit-learn)

Local Outlier Factor (LOF)

Local Outlier Factor(LOF)는 밀도 측정 방식의 비지도 알고리즘으로 어느 정도의 고차원의 데이터셋에서 사용할 수 있으며, 다변량 이상치 탐색법이다. LOF 알고리즘은 관측치가 이웃들(k-nearest neighbors)에 비해 주변과의 밀도가 낮을 때 이상치로 판별한다. 이상치 판별을 위해 각 데이터의 이상 정도(abnormality)를 나타내는 LOF score를 계산하는데, LOF score는 데이터 포인트(p)의 이웃들이 해당 포인트(p)에 비해 주변과 얼마나 밀도있는 지를 나타낸다. 정상치라면 이웃들과 비슷한 local density를, 이상치라면 이웃들보다 작은 local density를 가질 것이다.

 

관측치 p의 LOF = (k개 최근접 이웃들의 평균 local density) / (p의 local density)

 

LOF는 전체 데이터 분포에 비해서 포인트가 얼마나 밀도 있는지를 계산하는 것이 아니라 포인트 주변의 지역에 국한하여 밀도를 비교하는 것이므로 지역적인 밀도 편차(local density deviation) 측정이라 할 수 있다. 즉, 관측치가 전체 데이터셋에서 얼마나 동떨어져 있는지를 보는 것이 아니라, 주변 이웃, 클러스터로부터 얼마나 동떨어져 있는지를 측정한다. 따라서 판별된 이상치를 local outlier라고 부른다. 실제적으로 LOF 계산에 사용되는 수식은 아래에서 더 자세히 살펴볼 것이다.

 

Basic idea of LOF: comparing the local density of a point with the densities of its neighbors. A has a much lower density than its neighbors.

 

각 관측치의 LOF score를 원의 크기로 나타낸 것

k-nearest neighbors, k값

밀도 편차를 구할 지역을 국한하는데 쓰이는 k값은 보통 다음과 같이 결정되고, k-nearest neighbors의 거리를 통해 밀도를 측정한다.

 

1) 한개의 클러스터가 가져야하는 최소 관측치 개수보다 커야한다. 해당 클러스터와 비교했을 때 타 관측치가 local outliers로 판별될 수 있기 때문에  

2) smaller than the maximum number of close by objects that can potentially be local outliers

 

실제적으로 위와 같은 정보는 보통 알 수 없기 때문에, k=20으로 설정하고 이 경우 일반적으로 잘 작동한다고 한다. 데이터에서 이상치의 비율이 10% 초과로 높다면 k값은 더 커져야 한다. k값을 작게 설정할수록 알고리즘은 이상치에 더 민감해지고, 크게 설정할수록 무뎌져서 local outliers를 찾아내지 못할 수 있다.

LOF 계산

 

Reachability Distance (RD)

 

• RD(A, neighbor): A의 RD from neighbor. 포인트 A가 이웃으로부터 도달되어질 수 있는 거리
• 참고로 어떤 포인트(A)의 k개 최근접 이웃들은 모두 RD가 k-dist(A)로 같은데(RD(neighbor, A)), k개 이웃들이 모두 A로부터 같은 거리에 있다고 간주하는 것이다. 이는 최근접 이웃들 간의 statistical fluctuations를 줄여주기 위함이다. 

Local Reachability Density (LRD)

 

• LOF를 구하려는 포인트(A)의 k개 이웃들로부터의 RD 평균에 역수를 취한 것
• RD 평균이 클수록 A의 주변의 밀도가 낮음을 의미. 결과적으로 LRD는 RD 평균이 클수록 작아진다.
• LRD(A)는 A가 최근접 클러스터로부터 얼마나 떨어져있는지를 나타내는데 LRD가 클수록 최근접 클러스터가 가까이, 작을수록 멀리있음을 의미한다.
• 이웃들의 RD가 아닌 A의 RD를 사용함에 주의 ⇒ RD(A, neighbor)
  (참고로 위에서 말한 것처럼 k개 이웃들의 A로부터의 RD (RD(neighbor, A))의 평균은 결국 k-dist(A)임. 이럴 경우 LRD(A)는 결국 k-dist(A)의 역수가 되어버린다.)
• 공식에 쓰이는 거리 계산 방식은 problem-specific (e.g. Euclidean, Manhattan, Minkowski etc.)

<예시1>은 P와 3-최근접 이웃들인 $O_1$, $O_2$, $O_3$와의 거리가 가깝기 때문에 RD(P, Oi)가 작고, 결과적으로 LRD(P)가 커지게 된다. 반면 <예시2>는 P와 3-최근접 이웃들과의 거리가 멀기 때문에 RD(P, Oi)가 커지고 LRD(P)는 작은 값이 나온다. 앞서 말한 것처럼 LRD(P)가 클수록 최근접 클러스터가 가까이 있음을 나타내며, LOF값이 작아진다.

 

 

LOF 값의 의미

 

• LOF < 1: 이웃들보다 높은 밀도(Inliner) 
• LOF = 1: 주변의 밀도와 비슷
• LOF > 1: 이웃들보다 낮은 밀도(Outlier)

항상 위와 같은 기준으로 이상치 여부를 판단하는 것은 아니다. 만약 데이터셋에 이상치가 한 개라는 것을 알고 있는 상태라면 LOF 값이 최대인 관측치를 이상치로 판별할 것이다.

Illustration of the reachability distance. Objects B and C have the same reachability distance (k=3), while D is not a k-nearest neighbor

 

위는 k=3일 때 reachability distance를 나타낸 그림이며, 계산해보면 B와 C의 A로부터의 reachability distance는 같다. 위에서 설명한 것처럼 어떤 점 A의 k개 이웃들의 RD는 모두 k-dist(A)로 같기 때문이다.

 

RD(B, A) = max(k-dist(A), dist(B, A) = k-dist(A)

RD(C, A) = max(k-dist(A), dist(C, A) = k-dist(A)

sklearn.neighbors.LocalOutlierFactor

- scikit-learn의 LocalOutlierFactor 모델은 outlier detection과 novelty detection 두 가지 모두 가능한데, outlier detection을 할 때는 하이퍼파라미터 novelty를 False로, novelty 탐색을 할 때는 True로 설정하게 된다. outlier detection을 할 때 predict, decision_function, score_samples 메소드는 사용할 수 없고, fit_predict는 사용할 수 있다. 반대로 novelty detection 에서는 fit_predict를 사용할 수 없고, 전자의 메소드들은 novelty detection에서 새로운 unseen 데이터에만 사용할 수 있다. 

 

- 학습 데이터셋의 LOF score는 negative_outlier_factor_ 메서드로 알 수 있는데 음수로 변환되어 나온다. 정상치의 LOF는 1에 가깝고, 이상치의 LOF는 1보다 크기 때문에 negative_outlier_factor_값이 클수록 정상임을 의미한다.

LOF vs 다른 이상치 탐색 알고리즘

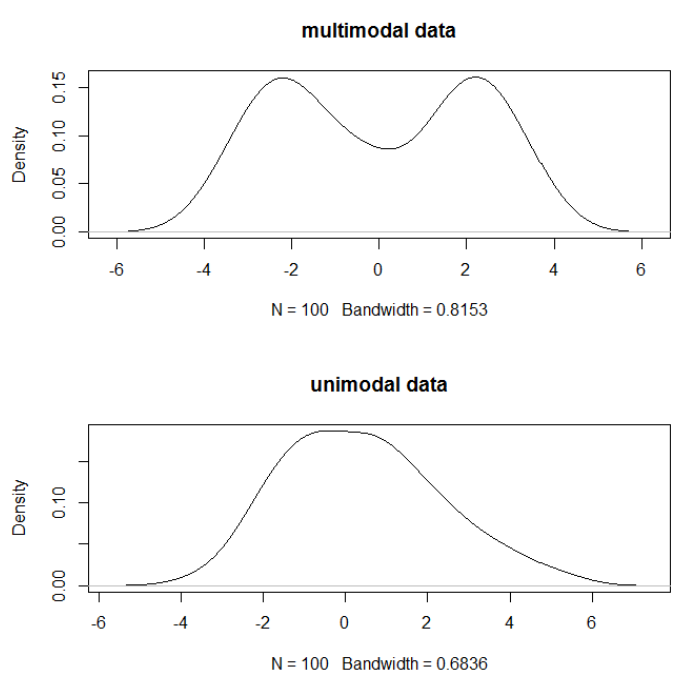
아래는 2차원 데이터셋에 각 이상치 탐색 알고리즘을 실행했을 때의 결과를 비교한 것이다. 데이터셋들은 한개나 두개의 mode(고밀도 지역)를 갖도록 하여 각 알고리즘이 multimodal 데이터셋을 잘 처리하는지를 보여주도록 하였다.

multimodal = 최빈값이 여러개, unimodal = 최빈값이 한 개

다른 알고리즘들과 다르게 LOF는 이상치와 정상치의 경계가 검은 선으로 구분되어 있지 않은데 앞서 말한 것처럼 outlier detection을 할때는 predict 메소드를 사용할 수 없기 때문이다. Isolation Forest와 LOF는 multimodal 데이터셋에서 꽤 잘 작동하고 있는 것으로 보이며, 다른 알고리즘들과 비교했을 때 LOF의 장점은 세번째 데이터셋에서 잘 나타나고 있다. 세번째 데이터셋은 두 mode(밀집지역)의 밀도가 서로 다른데 LOF는 지역성을 고려하여 이상치를 잘 찾아내고 있다. 이러한 장점은 LOF가 관측치(one sample)의 밀도를 주변 이웃들과만 비교한다는 데에서 온다.

LOF의 장점

• 이웃들과 비교했을 때 이상치인지 아닌지를 판단하므로 전체적인(global) 이상치뿐만 아니라 지역적 이상치(local outliers) 검출이 가능
• 데이터 개체들의 분포에 대한 가정이 필요하지 않으므로 개체들의 통계적 분포에 무관하게 이상치를 검출할 수 있다.
• 모든 관측치에 대해 이상치 정도(abnormality)를 단일 지표로 나타낼 수 있다.
• 데이터셋의 전반적인 밀도가 일정하지 않을 때 잘 작동한다.
• 데이터셋의 지역적, 전체적 특징을 모두 고려하므로 이상치들의 밀도가 서로 다른 데이터셋에서도 잘 작동한다.
• 지역적인 접근을 하므로 데이터셋의 다른 지역에서는 이상치로 판별되지 않는 포인트를 이상치로 찾아낸다.
  
  예를 들어 데이터셋 내 어떤 희박한 클러스터의 정상치들 간의 거리가 d이고, 다른 빽빽한 클러스터로부터 d의 거리만큼 떨어져있는 점 p1이 있다고 하자. global한 접근을 하는 알고리즘은 점 p1을 정상치로 판별하겠지만 LOF는 local outliers를 찾아내기 때문에 거리가 d로 같더라도 p1을 이상치로 판별해낼 수 있다.
  
  즉, 같은 거리이더라도 주변의 밀도에 따라 어떤 지역에서는 이상치로, 다른 지역에서는 정상치로 판별될 수 있는 것이다.

LOF는 P1과 P2를 Cluster 2에 대한 local outliers로 판별할 수 있다.

 

While the upper right cluster has a comparable density to the outliers close to the bottom left cluster, they are detected correctly.

LOF의 단점

• LOF 값은 몫(quotient-values)이기 때문에 값이 가지는 의미를 해석하기 어렵다. 보통 LOF가 1 이하면 정상치, 1 보다 크면 이상치라고 하지만 뚜렷한 threshold value가 없으므로 사용자가 데이터와 문제에 맞게 결정해야 한다.
  
  예를 들어 어떤 데이터셋에서는 LOF값 1.1의 포인트가 이상치일 수 있지만, local fluctuations가 심한 다른 데이터셋에서는 LOF값 2의 포인트가 여전히 정상치일 수 있다.
  
  이러한 기준의 차이는 LOF 알고리즘의 지역성(locality) 때문에 하나의 데이터셋 내에서도 나타날 수 있다.
• 계산 비용이 높다.
• 주변의 밀도가 높은 경우 LOF가 커져서 이상치가 아님에도 이상치로 판별하거나, 주변의 밀도가 낮은 경우 LOF가 작아져 이상치임에도 찾아내지 못하는 경우가 발생할 수 있다.

LOF의 단점을 개선하기 위한 다양한 extension들이 있다.

 

 

 

scikit-learn 공식문서

 

• sklearn.neighbors.LocalOutlierFactor
• 2.7. Novelty and Outlier Detection - 2.7.3.3. Local Outlier Factor
• Outlier detection with Local Outlier Factor (LOF) 
• Comparing anomaly detection algorithms for outlier detection on toy datasets

 

Novelty detection with LOF

 

• Novelty detection with Local Outlier Factor

 

 

Reference

1. 이상값 이상치 Outlier 탐지 

2. Local outlier factor - Wikipedia 

3. Outlier Detection Techniques: Simplified 

4. 4 Automatic Outlier Detection Algorithms in Python 

5. Local Outlier Factor (LOF) - Algorithm for outlier identification 

6. LOCAL OUTLIER FACTOR 

7. 7.2.4 R에서 LOF(Local Outlier Factor)로 이상치(Outlier) 찾기 

 

8. Outlier

9. Evaluation of outlier detection estimators -> LOF와 IsolationForest 모델 성능 평가